1. Background Knowledge

a. Fundamental Review of the Trading Book
b. Risk Types in the FRTB standardised approach

2. Relevant Risk Types for an EUR Equity Option

a. Equity Risk
b. General Interest Rate Risk
c. Default Risk Capital Charge

Fundamental Review of the Trading Book

The Fundamental Review of the Trading Book (FRTB) is a regulation introduced by the Basel Committee on Banking Supervision to address shortcomings in the regulation, supervision, and risk management of banks' trading book activities revealed in the aftermaths of the financial crisis 2007 - 2009. It aims to improve the banking sector's resilience by enhancing risk sensitivity, reducing variability in risk-weighted assets across banks, and ensuring capital adequacy and transparency.

Banks can choose between the standardised approach and the internal model approach. The latter detached the Value at Risk and introduced the Expected Shortfall at 97.5% confidence level as primary risk measure. Requirements for the internal model approach are high and expensive to implement. The regulation requires banks to implement the standardised approach in any case. Therefore, many banks currently enrolled for internal models are switching to the standardised approach.

Risk Types in the FRTB standardised approach

Under FRTB standardised approach, capital charges are categorized broadly into:

• Sensitivity Based Method (MAR 21)
  • General Interest Rate Risk (GIRR)
  • Credit spread risk (CSR): non-securitisations
  • CSR: securitisations (non-correlation trading portfolio, or non-CTP)
  • CSR: securitisations (correlation trading portfolio, or CTP)
  • Equity Risk
  • Commodity Risk
  • Foreign Exchange Risk
• Default Risk Capital Charge (MAR 22)
• Residual Risk Add On (MAR 23)

Sensitivity based methods utilize simple numerical approximations for the sensitivities to the respective risk factors. The default risk capital charge is built similar as expected loss (EL) used in the banking book: the jump to default value (loss given default (LGD) * exposure at default (EAD)) is multiplied by a risk weight that is determined by credit quality, e.g. 0.5% for credit quality AAA. Thus, if we interpret the risk weight as probability of default (PD) we can recover the well-known formula for expected loss: EL = PD*EAD*LGD. Residual risk add on is used for exotic underlying, where the above risk factors are not exhaustive to capture the risks.

In this article we focus on the equity capital charge of a EUR equity option. We chose this example since there are capital requirements from the full scope of risk factors defined in the regulation for equity while still having a relatively easy and well understood product.

Relevant Risk Types for an EUR Equity Option

Equity Risk

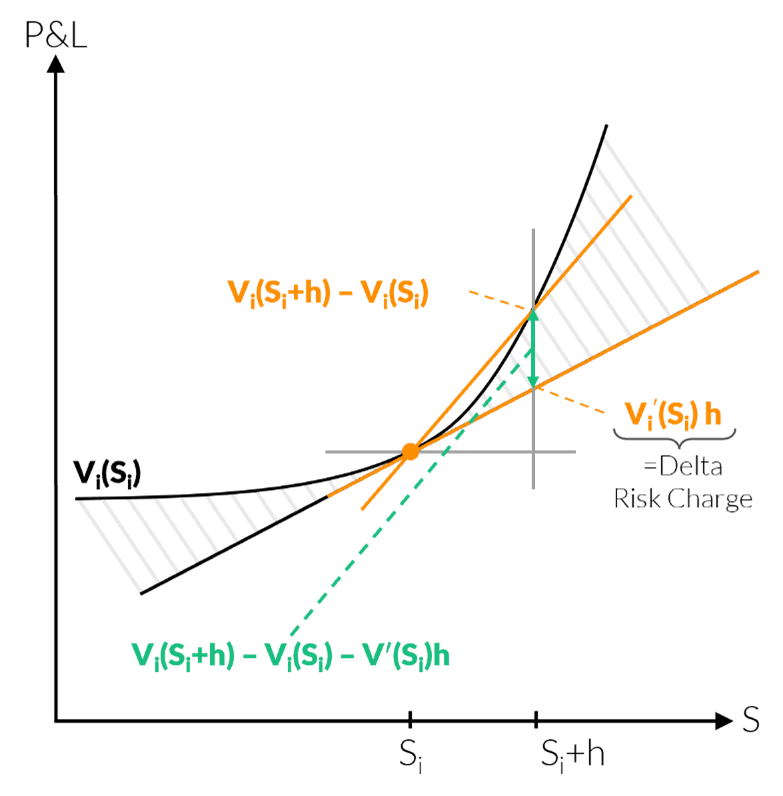
Equity risk focuses on changes in equity prices. The most important and largest contributor to the equity capital charge usually is equity delta. In context of FRTB equity delta is defined as the forward difference approximation of the first derivative of the pricing function with respect to the underlying equity spot price multiplied by the current price.

For a simple equity position equity delta is straight forward since it is a linear product with a slope of one. Equity delta is then just the current market value of the equity position. The same is true for forwards and futures. Since we have a time component in forwards and futures, additional to the delta risk charge we have an equity repo delta risk charge. It is defined as the first numerical derivative of the pricing function with respect to a one basis point parallel shift of the equity repo rate term structure. The implied repo rate for a given maturity can be replicated by buying the stock with borrowed money and sell a forward contract on the equity. The repo rate then is the difference of the forward rate to the borrowing rate. In case of certain dividend payments typically the repo rate is zero. Whenever there is uncertainty about dividend payments it is positive. The FRTB equity repo delta is well approximated by the backward difference approximation of the first derivative of the pricing function with respect to the forward rate.

For equity positions that carry an optionality in the underlying equity FRTB requires a curvature risk charge and a Vega risk charge in addition to the delta risk charge.

Curvature risk charge is calculated as an adjustment to the delta charge if the nonlinear behaviour of the position harms the P&L, otherwise it is set to zero. It is best motivated by considering gamma of a plain vanilla option, i.e. the second derivative of the pricing function with respect to the underlying equity. If you buy an ATM call option and keep your position delta neutral by selling shares, you will be long gamma. That is your option will gain more than the underlying equity in case of a price increase and will lose less in case of a price decrease. In this case the FRTB curvature risk charge is zero. If you sell an ATM call option and keep your position delta neutral by buying shares, you will be short gamma. That is the gain of the stock is less than the loss of the option in case of a price increase and the loss on the stock will be higher than the gain of the option in case of a price decrease. In this case the FRTB risk charge is based on the more severe loss scenario. The following two figures illustrate the two cases.

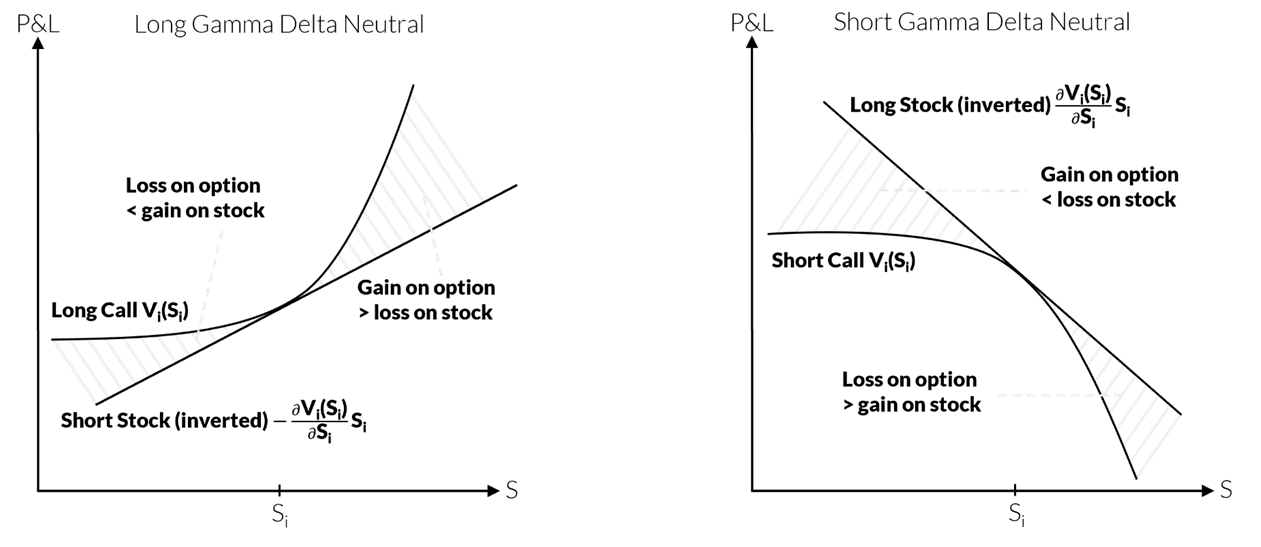
The measure for the risk charge in FRTB is closely related to the numerical approximation of gamma as we will see in the following. Let be the pricing function of the instrument, Let V_i be the pricing function of the i^th instrument, S_i the underlying equity price, ξ denote the remaining parameters of the pricing function and ' shall always denote the partial derivative w.r.t. the equity spot price. The finite difference approximation of gamma with the step size h is given by

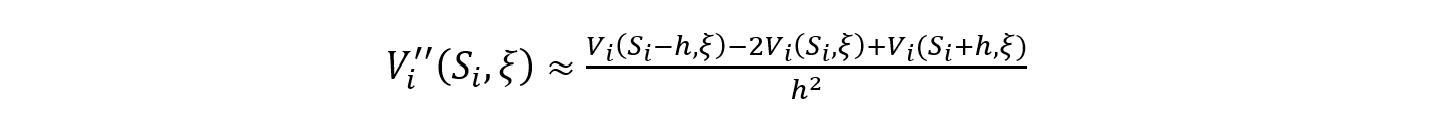
The curvature risk charge for the i^th instrument in the k^th bucket is based on the following

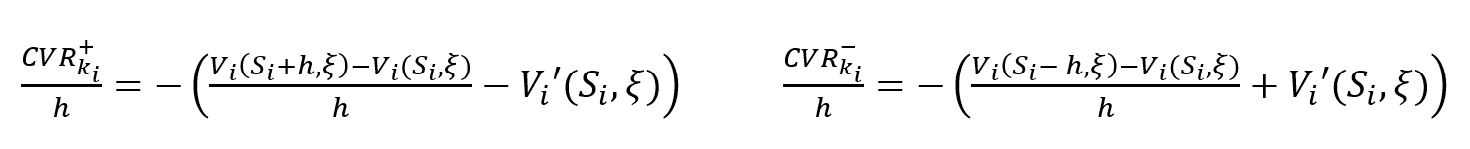
where h is set to the corresponding risk weight of the delta risk charge of the i^th instrument.

In total, the following relation between gamma and the intermediate results of the FRTB capital charge calculation holds

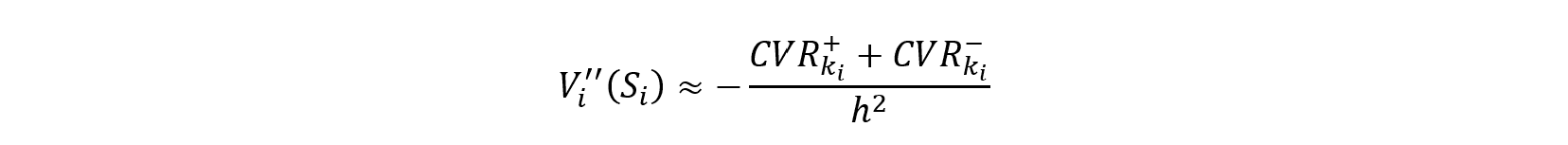
For an isolated position without aggregation effects the risk charge comes down to the larger of the CV Rs. In the following it is highlighted that curvature risk charge is an adjustment of delta risk charge.

If an equity option desk is delta gamma neutral the FRTB equity delta risk charge is close to zero. Curvature risk charge should also be close to zero depended on how well the curvature of short and long option positions set off via CV R+ and CV R-. For example, a gamma delta neutral position consisting of a long put, short call (ATM with same maturity and strike) and equity can have positive CV R- and thus a positive capital charge. This is basically a consequence of the hockey stick payoff profile of options.

Vega risk charge is simply the forward difference numerical approximation of the first derivative of the pricing function with respect to the implied volatility multiplied by the implied volatility and then weighted by the risk weight defined in the FRTB regulation. It is highest for ATM options and decreases as maturity approaches. It is supposed to capture that high volatility increases the risk to end up out of the money. Often risk managers incorporated the structure of the volatility smile into their risk assessments. However, the FRTB standardised approach only requires to consider parallel shifts in the volatility.

Note, for first-order sensitivities we must assume that the implied volatility remains constant.

General Interest Rate Risk

The interest rate environment is strongly connected to the economic conditions in a region. Total money supply, inflation rate, political decisions from central banks and governments, gross domestic product (GDP) growth and the degree of globalization are important risk drivers.

For equity options this risk factor plays a minor role but is naturally required as the potential cash flows are in the future. Market participants can read off the current interest rate environment from financial markets. It is market convention to use the option implied forward rate (can be obtained via a synthetic forward position using a long call and short put with the same strike and maturity) consistent with the risk neutral pricing approach used to derive the Black Scholes formula for example.

Default Risk Capital Charge

The risk charge aims to capture default risk that may not be captured by other measures. All exposures are mapped to the respective obligor and limited hedging recognition is allowed. In our case a call option would have a long exposure to the underlying equity and the capital charge would be the mark to market value of the option multiplied by some risk weight depended on the rating of the underlying equity. Note that the loss given default for equities is assumed to be one, which is why the long exposure is only multiplied by an assumed default probability (risk weight). A put option would have a short underlying exposure equal to the strike of the option. There is no capital charge if we are net short to an obligor.

Conclusion

The FRTB equity capital charge is well aligned with the trading activities of an equities desk. Delta hedges are fully recognised but from a capital charge perspective it may not be optimal to keep the desk delta gamma neutral. Since the risk weights set out in FRTB range from 15% - 70%, the numerical approximations tend to imply stress scenarios rather than normal market behaviour.

Overall, the capital charge for an equity option can be much higher than the market value of the option itself because the implied potential (probability weighted) equity exposure is recognised as if one would have a corresponding equity position.