06.05.2024 / 09:00
FRTB Standardised Approach – Sovereign Bonds
Financial Markets

Fundamental Review of the Trading Book
The Fundamental Review of the Trading Book (FRTB) is a regulation introduced by the Basel Committee on Banking Supervision to address shortcomings in the regulation, supervision, and risk management of banks' trading book activities revealed in the aftermaths of the financial crisis 2007 - 2009. It aims to improve the banking sector's resilience by enhancing risk sensitivity, reducing variability in risk-weighted assets across banks, and ensuring capital adequacy and transparency.
Banks can choose between the standardised approach and the internal model approach. The latter detached the Value at Risk and introduced the Expected Shortfall at 97.5% confidence level as primary risk measure. Requirements for the internal model approach are high and expensive to implement. The regulation requires banks to implement the standardised approach in any case. Therefore, many banks currently enrolled for internal models are switching to the standardised approach.
Risk Types in the FRTB standardised approach
Under FRTB standardised approach, capital charges are categorized broadly into:
Sensitivity Based Method (MAR 21)
General Interest Rate Risk (GIRR)
Credit spread risk (CSR): non-securitisations
CSR: securitisations (non-correlation trading portfolio, or non-CTP)
CSR: securitisations (correlation trading portfolio, or CTP)
Equity Risk
Commodity Risk
Foreign Exchange Risk
Default Risk Capital Charge (MAR 22)
Residual Risk Add On (MAR 23)
Sensitivity based methods utilize simple numerical approximations for the sensitivities to the respective risk factors. The default risk capital charge is built similar as expected loss (EL) used in the banking book: the jump to default value (loss given default (LGD) * exposure at default (EAD)) is multiplied by a risk weight that is determined by credit quality, e.g. 0.5% for credit quality AAA. Thus, if we interpret the risk weight as probability of default (PD) we can recover the well-known formula for expected loss: EL = PD * EAD * LGD.
Residual risk add on is used for exotic underlying, where the above risk factors are not exhaustive to capture the risks.
Relevant Risk Types for a German Government Bond
General Interest Rate Risk
If we receive cash flows in the future, we usually require a premium to compensate for our opportunity costs of not having it today already.
If we assume that our counterparty carries no default risk, our opportunity costs could be the interest rate we could have earned by lending money to the German government.
When we want to know the present value of our future receivable cash flows, we can use this “opportunity cost” discounting rate to translate these cash flows to today.
General Interest Rate Risk (GIRR)
The interest rate environment is strongly connected to the economic conditions in a region. Total money supply, inflation rate, political decisions from central banks and governments, gross domestic product (GDP) growth and the degree of globalization are important risk drivers.
Market participants can read off the current interest rate environment from financial markets. Often government bond rates, interbank lending rates or central bank overnight rates serve as benchmark.
Credit Spread Risk
Credit Spread is issuer-specific and reflects the credit quality of the issuer. It can be obtained as the difference of issuer yield to “risk free” yield implied by government bonds with similar tenor for example. For large corporations with many outstanding bonds with different tenors it is possible to back out a credit spread curve from the prices.
Another way to obtain the credit spread is by using credit default swaps (CDS) if they are traded for the issuing company. Normally CDS are quoted as credit spread, i.e., the yearly premium the protection buyer must pay. Of course, there is a close relation between the bond credit spread and the one from CDS. However, be cautious as there is basis if you want to hedge your credit spread position in a CDS with Bonds and vice versa.
Example from the EUR Corporate investment grade (IG) Bond Market
This section aims to shed some light on the question of why we need to split the yield curve into GIRR and CSR in FRTB. We argue that this is market practice and explain it via the EUR Corp. IG Bond primary market, because we find it more illustrative for our argument than the Sovereign bond primary market. The respective auctions work differently and a split between CSR and GIRR is much more natural for corporate bonds
The primary bond market is an auction organized by banks for companies that aim to issue bonds to investors. Issuers aim for the lowest yield at which they can still secure their funding needs. Investors seek fair compensation for their risk-taking. Bonds always sell just below par and the target of the auction is to find the coupon rate.
The auction price quotes of an EUR Corp. IG bond are a sum of the European mid swap rate (general interest rate) plus a company specific credit risk premium (credit spread). However, if the issuer has liquid bonds trading in the secondary market (exchange) it is possible to interpolate the fair value of the newly issued bond implied by the market. Investors typically require a net issue premium (residual risk) so that the yield of the new issue is higher than the fair par yield implied by the market.
In principle the auction would work equally well in many cases if we just took market implied yields. Why then split the quotes into the two components? Because credit quality is crucial for investors and if there are no outstanding bonds of the issuing company in the market the credit spread component must be determined in another way (for example internal ratings of banks). Further, the exposure profile to different industry sectors requires the yield to be split into an industry sector specific component and a market component.
Since differentiating between systemic interest rate (GIR) and idiosyncratic interest rate (CS) is common market practice it is natural to consider GIRR and CSR separately in FRTB as well.
Extensive Risk Measure
Parallel shifts in interest rates refer to a situation where all interest rates across the yield curve move by the same amount in the same direction, either upwards (an increase) or downwards (a decrease). The yield curve represents the relationship between interest rates (or yields) and the time to maturity for debt securities of similar credit quality.
Empirically, parallel shifts in interest rates are most common. However, opposite movements of short- and long-term rates or bowing also appear frequently. Our goal is it to find a risk measure that incorporates the observable behaviour of (risk free) interest rates.
Example of a 10-Year German Government Bond
For a 10-year German government bond, the most important risk is interest rate risk. This is the risk of potential loss from fluctuations in interest rates, which inversely affect bond prices (as interest rates rise, bond prices fall, and vice versa).
According to the regulation, for European banks there is no default risk charge for sovereigns of domestic currency. But there is a credit spread risk charge.
Calculating Capital Requirements for a 10-Year German Government Bond
Let us first consider the yield curve implied by triple A rated European Sovereigns in Figure 1. We compare the curve as of 10JAN2024 with a more recent curve as of 4APR2024. We can observe a parallel shift of the curve for tenors between 5- and 17-years residual maturity. For short tenors the yields almost did not change and remain at high level while at long tenors it increased slower than in the medium tenors. Bear in mind that the short residual maturities are rather liquid while very long residual maturities are less liquid. Further, most of the bond primary market happens in the medium tenors usually implying a deep secondary market in this segment.
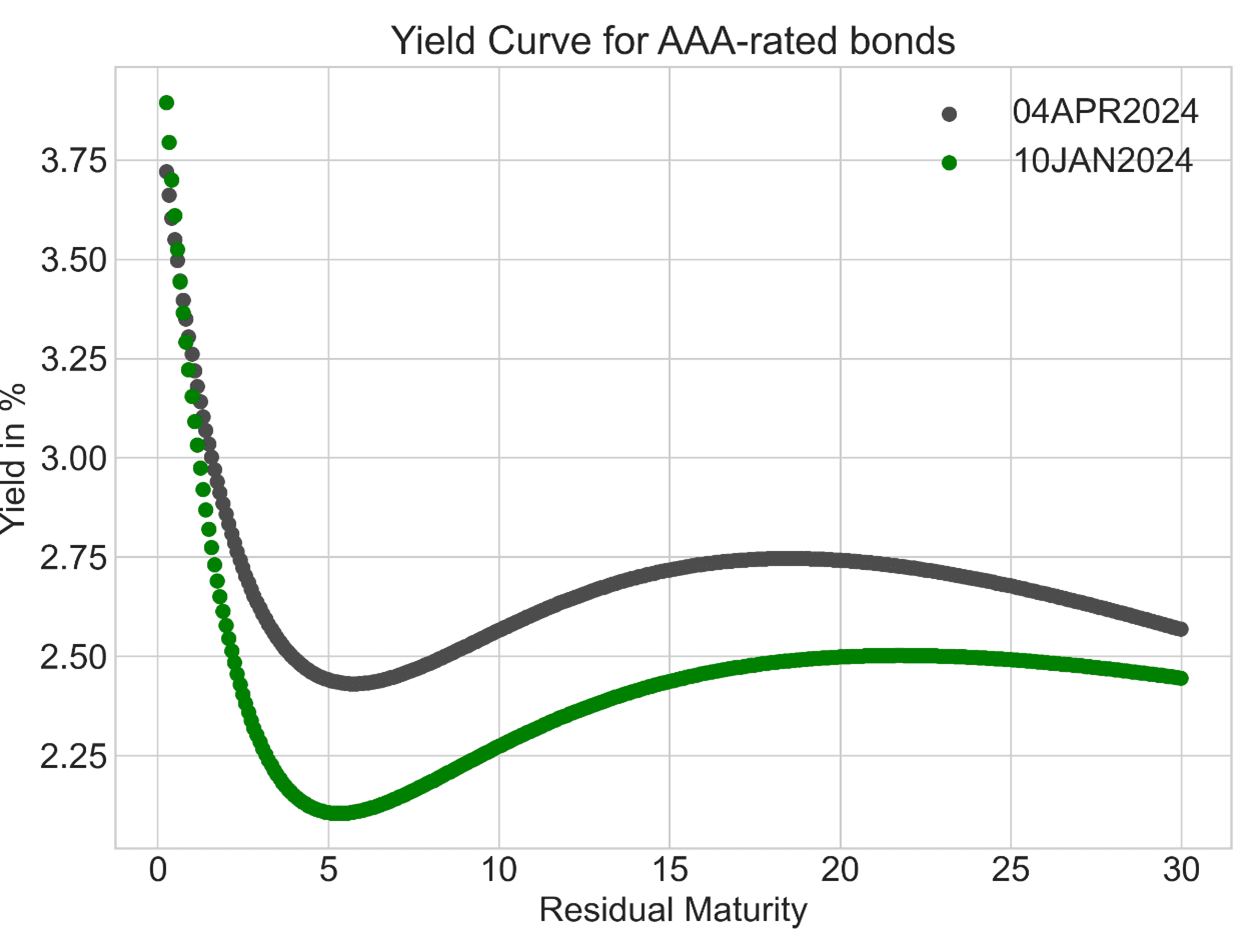
Figure 1: ECB published data. https://www.ecb.europa.eu/stats/financial_markets_and_interest_rates/euro_area_yield_curves/html/index.en.html
Recall that empirical research showed, parallel shifts in interest rates are most common. However, opposite movements of short- and long-term rates or bowing also appear frequently.
The standardised approach in FRTB in parts incorporates this in the risk measures for GIRR and CSR by splitting the sensitivities into tenor buckets and providing a correlation matrix to capture the co-movement of bucket sensitivities. For example, the tenor buckets for GIRR are 0.25 years, 0.5 years, 1 year, 2 years, 3 years, 5 years, 10 years, 15 years, 20 years and 30 years.
For each bucket, a PV01 (present value of a basis point) is calculated by key rate shifts using the (finite difference) Euler method. For example, the GIRR sensitivity has the following form:
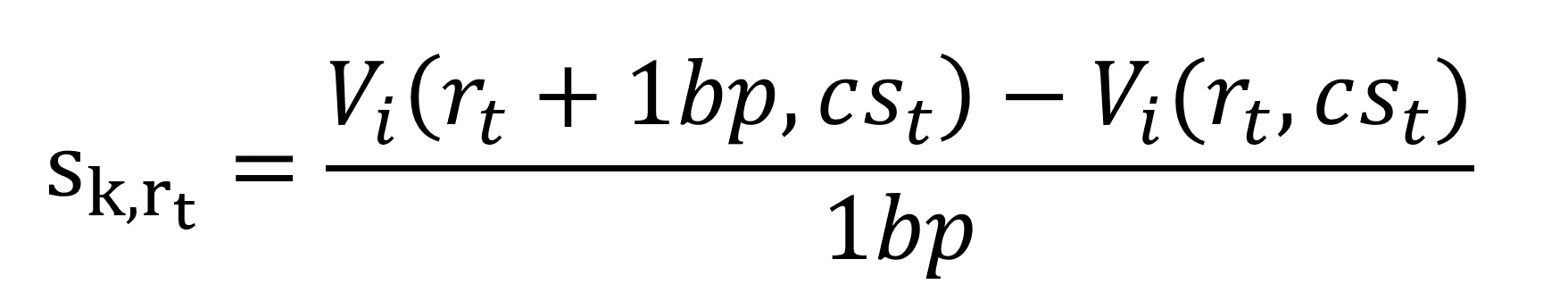
Where V_i is the market value of the instrument, i^th is the interest rate at time t, cs_t is the credit spread at time t and k indicates the tenor bucket. If cash flows do not occur at the exact tenor of a bucket a linear interpolation is done, see Figure 2.
Let’s consider the 10Y German Government bond issues at 10JAN2024 (ISIN: DE000BU2Z023). The first cash settlement is on the 15FEB2025 with a coupon rate of 2,20% and yearly coupon frequency. Now consider the 3 year bucket (function f_4 in Figure 2): every cash flow between 2 and 5 years is discounted by r_cashflow date + f_4 (cashflow date) in the calculation of V_i (r_3Y + 1bp, cs_3Y). Then we get the sensitivity by differencing the “shifted” present value with the market value and dividing by 1bp. This would be the sensitivity of tenor bucket 3 years if our portfolio only consists of the one instrument.
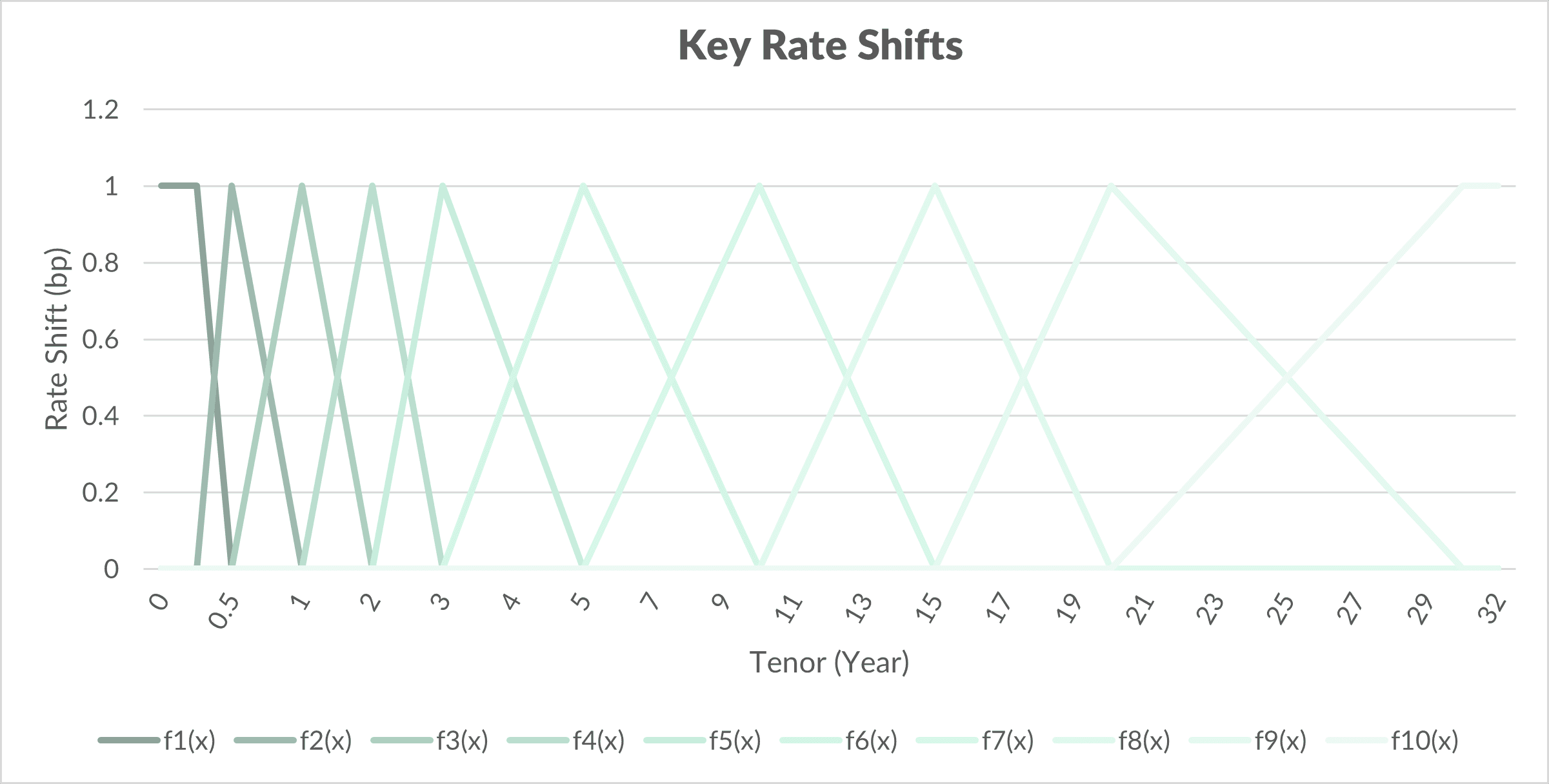
Figure 1: Illustration of Key Rate Shifts.
As a last calculation step the vector of sensitivities is weighted with the risk weights defined in FRTB regulation. The capital charge is then the square root of a matrix vector product of the weighted sensitivities with the correlation matrix (of the form sqrt(x^TMx)).
The credit spread risk component is calculated like GIRR but with fewer buckets and different risk weights. See MAR 21 for further information on the weights and the correlation matrix.
Conclusion
The inclusion of the observable market behaviour of interest rates within the risk measure in the FRTB standardised approach enhances the accuracy and relevance of risk assessments.
The capital charge for a European bank for holding a 10-year German Government Bond in their trading book is approximately 10% of the bonds notional value. This buffer enhances resilience of banks against potential market volatilities and adds to the stability of the financial system.


